Para resolver una raíz cuadrada seguiremos los pasos del siguiente ejemplo:
1. Si el radicando tiene más de dos cifras separamos las cifras en grupos de dos, empezando por la derecha.
2. Calculamos la raíz cuadrada entera o exacta, del primer grupo de cifras por la izquierda, en este caso el (8)
Nos hacemos la pregunta: ¿qué número elevado al cuadrado da 8?
Vemos que 8 no es un cuadrado perfecto, pero está comprendido entre dos cuadrados perfectos: 4 y 9.
Entonces, tomaremos la raíz cuadrada del cuadrado perfecto menor al (8), es decir la raíz cuadrada del 4, quedando2, y lo colocamos en la casilla correspondiente.
3. El cuadrado de la raíz obtenida 2 (es decir 4) se resta al primer grupo de cifras que aparecen en el radicando (8)
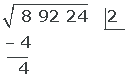En otras palabras, el cuadrado de 2 es 4, se lo restamos a 8 y obtenemos 4.
4. Bajamos el siguiente grupo de cifras del radicando, separando del número formado (492) la primera cifra a la derecha (2) y dividiendo lo que resta entre el doble de la raíz 2, es decir 2(2)=4.
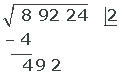En otras palabras:
- Bajamos 92, siendo la cantidad operable del radicando: 492.
- Separamos la 1ª cifra a la derecha (2) y nos quedamos con 49.
- Dividimos 49 entre el doble de la raíz obtenida anteriormente 2 · 2 = 4
- Como el resultado de 49 : 4 es mayor que 9, tomamos como resultado al 9
Nota: Tomamos 9 siempre que el resultado de la división (49:4) sea mayor que 9
5. En otra fila debajo de la raíz colocamos el doble de la misma (4). A continuación, se coloca el cociente que se obtenga (9) . Y luego el número obtenido (49) se multiplica por dicho cociente (9). Después, se resta (441) a la cantidad operable (492) del radicando.
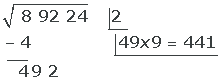
- Colocamos en otra fila el doble de la raíz, que en este caso es 4.
- Colocamos el cociente obtenido (9) a continuación del 4, obteniendo así el número 49.
- Multiplicamos 49 por 9 y obtenemos 441
- Restamos 441 a 492 (que es la cantidad operable del resultado).
Nota: Si hubiésemos obtenido un valor superior a la a la cantidad operable del radicando, habríamos probado por 8, por 7... hasta encontrar un valor inferior.
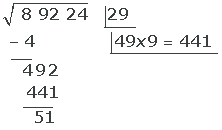
Nota: Si el resultado de hacer 49 · 9 hubiese sido mayor que 492, habríamos probado a hacer 49 · 8, 49 · 7,...
6. El cociente obtenido (9) es la segunda cifra de la raíz, quedando (29).
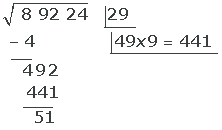
7. Bajamos el siguiente par de cifras y repetimos los pasos anteriores.
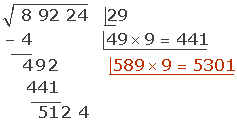
Como 5301 > 5124, probamos por 8.
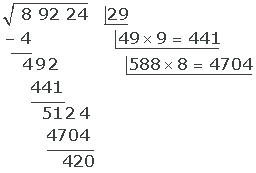
Finalmente, subimos el 8 a la raíz.
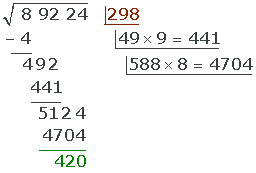
Y con esto terminamos el proceso.
8. Prueba de la raíz cuadrada. Para que el resultado sea correcto, se tiene que cumplir:
Y efectivamente los valores obtenidos lo cumplen:
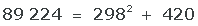
Ver video de como se resuelve raíz cuadrada, aunque lo normal es utilizar la calculadora: