POLIEDRO IRREGULAR
Los poliedros irregulares son poliedros cuyas caras son polígonos no todos iguales.
PRISMA
Un prisma es un poliedro cuya superficie está formada por dos caras iguales y paralelas llamadas bases y por caras laterales (tantas como lados tienen las bases) que son paralelogramos.
Por el número de lados de las bases el prisma recibe su nombre: triangular, cuadrilátero (paralelepípedo), pentagonal, etc. La altura de un prisma es la distancia entre las bases.
ELEMENTOS DEL PRISMA
En un prisma se pueden diferenciar los siguientes elementos:
-
- Bases (B): polígonos cualquiera. Cada prisma tiene dos bases, siendo ambas iguales y paralelas.
- Caras (C): los paralelogramos de los laterales y las bases.
- Altura (h): distancia entre las dos bases del prisma. En el caso del prisma recto la longitud de la altura h y la de las aristas de las caras laterales coinciden.
- Vértices (V): puntos donde confluyen las caras del prisma.
- Aristas (A): cada uno de los lados de las caras.
- Diagonales (D): segmentos que unen dos vértices que pertenecen a caras diferente
Video prisma
Video Poliedro: prismas
PIRÁMIDES
Una pirámide es un poliedro irregular cuya superficie está formada por una base que es un polígono cualquiera y caras laterales triangulares que confluyen en un vértice que se denomina ápice (o vértice de la pirámide). Las pirámides tienen tantos triángulos en las caras laterales como aristas tiene la base.
Elementos de la pirámide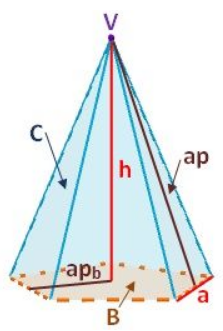
En una pirámide se pueden diferenciar los siguientes elementos:
- Base (B): polígono cualquiera. Es la única cara que no toca al vértice de la pirámide.
- Caras (C): los triángulos de los laterales y la base.
- Aristas (a): segmentos donde se encuentran dos caras de la pirámide. Podemos distinguir: aristas laterales, que son las que llegan al vértice (o ápice) y aristas básicas, que están en la base.
- Altura (h): distancia del plano de la base al vértice de la pirámide.
- Vértice de la pirámide (V): punto donde confluyen las caras laterales triangulares. También se llama ápice.
- Apotema de la pirámide (ap): distancia del vértice a un lado de la base. Solo existe en las pirámides regulares. Puesto que en este caso las caras laterales son isósceles, la apotema de la pirámide es también la altura de las caras laterales.
TIPOS DE PIRAMIDE
Las pirámides se pueden clasificar mediante cuatro criterios:
- Número de lados de la base
Las pirámides se pueden clasificar según el número de lados que tiene su base:
- Pirámide triangular: la base es un triángulo (3 lados).
- Pirámide cuadrangular: la base es un cuadrilátero (4 lados).
- Pirámide pentagonal: la base es un pentágono (5 lados).
- Pirámide hexagonal: la base es un hexágono (6 lados).
- Regular o irregular
- Pirámide regular: una pirámide es regular si la base es un polígono regular y a su vez es una pirámide recta. Las caras laterales son triángulos isósceles e iguales entre sí.
- Pirámide irregular: cuando la base es un polígono irregular o bien es una pirámide oblicua.
- Recta u oblicua
- Pirámide recta: la pirámide es recta cuando todas sus caras laterales son triángulos isósceles. En este caso, la recta perpendicular a la base que pasa por el vértice de la pirámide corta a la base por el centro del polígono.
- Pirámide oblicua: la pirámide es oblicua cuando no todos los triángulos laterales son isósceles.
- Convexa o cóncava
- Pirámide convexa: la pirámide es convexa si la base es un polígono convexo.
- Pirámide cóncava: la pirámide es cóncava si el polígono de la base es cóncavo.
TRONCO DE PIRÁMIDE
El tronco de pirámide es un poliedro formado por dos caras paralelas, que son las bases, y varias caras laterales, que son trapecios. Ambas bases tienen el mismo número de lados y tiene tantas caras laterales como lados tienen sus bases.
Está formado por el sólido inferior resultante de seccionar una pirámide con un plano intermedio y paralelo a su base.
Video Poliedro: pirámides